ANALISIS MATEMATICO Y PROBABILIDADES

• FACTORIAL DE UN NUMERO:
  
  
  Para todo numero natural  n, se llama n factorial o factorial de n al producto de todos los naturales desde 1 hasta n: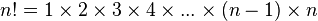
  

Ejemplo:
6!=6·5·4·3·2·1=720

• Variaciones

Se llama variaciones ordinarias de m elementos tomados de n en n (m ≥ n) a los distintos grupos formados por n elementos de forma que:

1. No entran todos los elementos.
2.  Sí importa el orden.
3. No se repiten los elementos.

Permutaciones

Hay dos tipos de permutaciones:

1. Se permite repetir: como la cerradura de arriba, podría ser "333".
2. Sin repetición: por ejemplo los tres primeros en una carrera. No puedes quedar primero y segundo a la vez.

•   Permutaciones con repetición

Son las más fáciles de calcular. Si tienes n cosas para elegir y eliges r de ellas, las permutaciones posibles son:

n × n × ... (r veces) = n^r

 
Ejemplo

10 × 10 × ... (3 veces) = 10³ = 1000 permutaciones

• Permutaciones sin repetición

En este caso, se reduce el número de opciones en cada paso.
ejemplo

16 × 15 × 14 × 13 ... = 20,922,789,888,000

Combinaciones

También hay dos tipos de combinaciones (recuerda que ahora el orden no importa):

1. Se puede repetir: como monedas en tu bolsillo (5,5,5,10,10)
2. Sin repetición: como números de lotería (2,14,15,27,30,33)

1. Combinaciones con repetición

En realidad son las más difíciles de explicar, así que las dejamos para luego.

2. Combinaciones sin repetición

Así funciona la lotería. Los números se eligen de uno en uno, y si tienes los números de la suerte (da igual el orden) ¡entonces has ganado!
La manera más fácil de explicarlo es:

• imaginemos que el orden sí importa (permutaciones),
• después lo cambiamos para que el orden no importe.

Ejemplo.

 

                             3! = 3 × 2 × 1 = 6

(Otro ejemplo: 4 cosas se pueden ordenar de 4! = 4 × 3 × 2 × 1 = 24 maneras distintas, ¡prueba tú mismo!)

PROFECION :TURISMO Y HOTELERIA

Trabajar en hotelería y turismo requiere de algunas habilidades específicas acordes a la industria que se llama industria de la hospitalidad.  Para trabajar en turismo y hotelería, es necesario ser extrovertido, disfrutar de la relación con las personas, sacrificar horarios para desarrollar una carrera (cumpleaños, fin de año, navidades, feriados, etc.) poder trabajar en equipo y orientación al servicio.

Las competencias básicas para trabajar en esta industria son:

1) Orientación al servicio. Tener claro que la esencia del trabajo tiene que ver con la asistencia a los clientes.
2) Que aprecie estar en contacto con personas. Tanto en equipo como con clientes, cara a cara, es el mayor desafío de este trabajo.
3) Abiertos a diferentes culturas. Deben estar abiertos a asistir a un japónes, a un brasileño o a un árabe. La flexibilidad para desenvolverse entre clientes de diferentes países y la apertura necesaria para asimilar diferentes pedidos.
4) Trabajar en equipo. El trabajador de hotelería y turismo trabaja con otros pares de diferentes áreas de un hotel o proveedores, por lo tanto debe aceptar que el trabajo en equipo es fundamental.
5) Ser creativos e innovadores. Para buscar soluciones a clientes diferentes, cada día es un desafío diferente en esta industria.
6) Interés en aprender idiomas. En Argentina hay una barrera idiomática, donde los jóvenes tienen poco o escaso interés en desarrollar el conocimiento en otros idiomas.
7) Buena presencia. No significa ser guapo. Sino mantener el aseo y prolijidad personal al día y la pulcritud en la vestimenta en todo momento

IDENTIDADES TRIGONOMETRICAS

      DEFINICION :  son   igualdades  que se establece a relacionar las razones trigonometricas unas con otras .

  CIRCULO TRIGONOMETRICO :

      Formulas fundamentales

RECIPROCRAS	POR COCIENTE	PITAGORICAS
Sen x . csec x=1 Cos x . sec x =1 Tg x. ctg x =1	Tg x =  sen x/cos x             Ctg x = cos x /sen x	Sen 2 x  + cos2  x=1 Sec2 x  –  tg2 x= 1 Csec 2 x - ctg2  x =1

TRIGONOMETRIA

La trigonometría es el estudio de las razones trigonométricas: seno, coseno; tangente, cotangente; secante y cosecante.

1. SISTEMA DE MEDIDAS ANGULARES 

• Sistema sexagesimal : Sistema de 360º su unidad es el grado sexagesimal  .

• Sistema ciclico : Es un angulo con vertice en el centro de una circuferencia y cuyos lados abarcan un arco de longitud igual al radio de la circuferencia a este sistema se le conoce como angulo unidad es el radian.

• Sistema centesimal :Resulta de dividir el ángulo recto en 400 partes iguales .

FIGURAS INSCRITAS Y CIRCUNSCRITAS EN LA CIRCUNFERENCIAS

•  Figuras inscritas: Es cuando un polígono está dentro de una circunferencia, cuando cada uno de los vértices de la figura inscrita toca los lados respectivos de la figura en la que se inscribe y cuando el polígono está inscrito en un círculo, cuando cada ángulo de la figura inscrita toca la circunferencia del círculo.

•  Figuras circunscritas:Es la figura que  está circunscrita en torno de otra figura, cuando cada lado de la figura circunscrita toca los vértices respectivos de la figura a la que circunscribe.

        TRIANGULO EQUILATERO INSCRITO EN UN CIRCULO

 

 

 

 

 

 

 

 

 

 

CUADRADO INSCRITO  EN UNA  CIRCUNFERENCIA