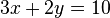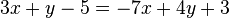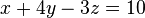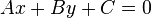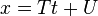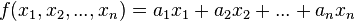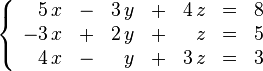martes, 23 de noviembre de 2010
MEDIDAS DE DISPERSION
Muestran la variabilidad de una distribución, indicando por medio de un número, si las diferentes puntuaciones de una variable están muy alejadas de la media. Cuanto mayor sea ese valor, mayor será la variabilidad, cuanto menor sea, más homogénea será a la media. Así se sabe si todos los casos son parecidos o varían mucho entre ellos.
medidas de tendencia
- Media aritmética. La media aritmética es el valor obtenido por la suma de todos sus valores dividida entre el número de sumandos
- Media ponderada. La mediana es un valor de la variable que deja por debajo de sí a la mitad de los datos, una vez que éstos están ordenados de menor a mayor.Por ejemplo, la mediana del número de hijos de un conjunto de trece familias, cuyos respectivos hijos son: 3, 4, 2, 3, 2, 1, 1, 2, 1, 1, 2, 1 y 1, es 2, puesto que, una vez ordenados los datos: 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 4, el que ocupa la posición central es 2:
- Media geométrica.
- Media armónica.
- Mediana. La mediana es un valor de la variable que deja por debajo de sí a la mitad de los datos, una vez que éstos están ordenados de menor a mayor.Por ejemplo, la mediana del número de hijos de un conjunto de trece familias, cuyos respectivos hijos son: 3, 4, 2, 3, 2, 1, 1, 2, 1, 1, 2, 1 y 1, es 2, puesto que, una vez ordenados los datos: 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 4, el que ocupa la posición central es 2:
- Moda. La moda es el dato más repetido, el valor de la variable con mayor frecuencia absoluta.En cierto sentido la definición matemática corresponde con la locución "estacv r de moda", esto es, ser lo que más se lleva.
lunes, 22 de noviembre de 2010
ecuaciones con una variable
Una ecuación es una igualdad de dos expresiones matemáticas. Una ecuación de primer grado en una variable es una ecuación en la que aparece una variable elevada al exponente uno. A estas ecuaciones también se le conocen como
Resolver una ecuación de primer grado en una variable consiste en hallar el valor de la variable que hace cierta la igualdad. A este valor se le conoce como
5(2) – 3 = 3(2) + 1
10 – 3 = 6 + 1
7 = 7 Cierto
martes, 16 de noviembre de 2010
Una ecuación de primer grado o ecuación lineal es un planteamiento de igualdad, involucrando una o más variables a la primera potencia, que no contiene productos entre las variables, es decir, una ecuación que involucra solamente sumas y restas de una variable a la primera potencia. En el sistema cartesiano representan rectas. Una forma común de ecuaciones lineales es:
y = m .x + b
Donde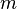 representa la pendiente y el valor de
representa la pendiente y el valor de 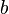 determina la ordenada al origen (el punto donde la recta corta al eje y).
determina la ordenada al origen (el punto donde la recta corta al eje y).
Las ecuaciones en las que aparece el término (llamado rectangular) no son consideradas lineales.
(llamado rectangular) no son consideradas lineales.
Ecuación general
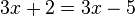 .
.
Adicionalmente podría haber más de dos variables, en ecuaciones simultaneas.


donde a es cualquier escalar. También se llama a f operador lineal
y = m .x + b
Donde
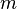 representa la pendiente y el valor de
representa la pendiente y el valor de 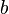 determina la ordenada al origen (el punto donde la recta corta al eje y).
determina la ordenada al origen (el punto donde la recta corta al eje y).Las ecuaciones en las que aparece el término
 (llamado rectangular) no son consideradas lineales.
(llamado rectangular) no son consideradas lineales.Algunos ejemplos de ecuaciones lineales :
Formas de ecuaciones lineales
Formas complejas como las anteriores pueden reescribirse usando las reglas del álgebra elemental en formas más simples. Las letras mayúsculas representan constantes, mientras x e y son variables.Ecuación general
-
- Aquí A y B no son ambos cero. Representa una línea en el cartesiano. Es posible encontrar los valores donde x e y se anulan.
- Ecuación segmentaria o simétrica
-
- Aquí E y F no deben ser cero. El gráfico de esta ecuación corta al eje X y al eje Y en E y F respectivamente.
- Forma paramétrica
- Dos ecuaciones que deben cumplirse de manera simultanea, cada una en la variable t. Puede convertirse a la forma general despejando t en ambas ecuaciones e igualando.
- Casos especiales:
- Un caso especial es la forma estándar donde
 y
y  . El gráfico es una línea horizontal sin intersección con el eje X ó (si F = 0) coincidente con el ese eje.
. El gráfico es una línea horizontal sin intersección con el eje X ó (si F = 0) coincidente con el ese eje.
- Otro caso especial de la forma general donde
 y
y  . El gráfico es una línea vertical, interceptando el eje X en E.
. El gráfico es una línea vertical, interceptando el eje X en E.
- En este caso, todas las variables fueron canceladas, dejando una ecuación que es verdadera en todos los casos. La forma original (no una tan trivial como la del ejemplo), es llamada identidad. El gráfico es todo el plano cartesiano, ya que lo satisface todo par de números reales x e y.
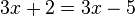 .
.Adicionalmente podría haber más de dos variables, en ecuaciones simultaneas.
Ecuación lineal en el espacio n-dimensional
Las funciones lineales de varias variables admiten también interpretaciones geométricas. Así una función lineal de dos variables de la formaSistemas de ecuaciones lineales
Los sistemas de ecuaciones lineales expresan varias ecuaciones lineales simultaneamente y admiten un tratamiento matricial. Para su resolución debe haber tantas ecuaciones como incógnitas y el determinante de la matriz ha de ser real y no nulo. Geométricamente corresponden a intersecciones de líneas en un único punto (Sistema lineal de dos ecuaciones con dos incógnitas), planos en una recta (dos ecuaciones lineales de tres incógnitas) o un único punto (tres ecuaciones lineales de tres incógnitas). Los casos en los que el determinante de la matriz es nulo no poseen solución.Linealidad
Una función es lineal si solo se cumple con la siguiente proposición:

donde a es cualquier escalar. También se llama a f operador lineal
Suscribirse a:
Entradas (Atom)