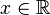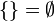En matemáticas, una función,[1] aplicación o mapeo f es una relación entre un conjunto dado X (el dominio) y otro conjunto de elementos Y (el codominio) de forma que a cada elemento x del dominio le corresponde un único elemento del codominio f(x). Se denota por:
SIMBOLO:
CLASES DE FUNCION
- la función es suprayectiva o sobreyectiva si, y sólo si, la ecuación (*) siempre tiene al menos una solución.
- la función es inyectiva si, y sólo si, la ecuación (*) tiene a lo más una solución.
- la función es biyectiva cuando, y sólo cuando, es inyectiva y suprayectiva a la vez.
Aplicación inyectiva y no sobreyectiva
En una función inyectiva, cada elemento imagen tiene única preimágen. Un función que no sea inyectiva, tendrá al menos dos elementos diferentes del dominio que tienen la misma imagen.
Aplicación no inyectiva y sobreyectiva
Una aplicación no inyectiva tiene al menos un elemento imagen que tiene dos o más orígenes y una sobreyectiva todos los elementos del conjunto final tienen al menos un elemento origen.
Aplicación inyectiva y sobreyectiva (biyectiva)
Si una aplicación es inyectiva y sobreyectiva simultáneamente, se denomina biyectiva. Por ser inyectiva los elementos que tienen origen tienen un único origen y por ser sobreyectiva todos los elementos del conjunto final tienen origen.
En el diagrama de Venn el conjunto A es el de las aplicaciones inyectiva y el conjunto B el de las aplicaciones sobreyectiva, las aplicaciones biyectiva, que son inyectiva y sobreyectiva, será la intersección de A y B.
Aplicación no inyectiva y no sobreyectiva
Una aplicación no inyectiva tendrá al menos un elemento imagen que tenga dos o más orígenes y una no sobreyectiva tendrá al menos un elemento del conjunto final que no tenga elemento origen. Este tipo de aplicaciones no tiene un nombre específico y quizá sean las que presenten, desde el punto de vista matemático, un menor interés.
Para esta aplicación los conjuntos
X e
Y no son comparables, y no podemos plantear ningún supuesto sobre su cardinalidad, partiendo de su comparación, ni sobre su número de elementos.
En el diagrama de Venn corresponden a las aplicaciones que no pertenecen a
A y no pertenecen a
B, esto es las que no pertenecen a la unión de
A y
B.
![[a, b] \,](http://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png)
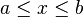
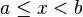
![]a, b] \ \ \mathrm{ \acute o } \ \ (a, b] \!](http://upload.wikimedia.org/math/0/1/8/0189f84b7a0ea78dbc527c545d8c9598.png)
![]a, b[ \ \ \mathrm{ \acute o } \ \ (a, b) \!](http://upload.wikimedia.org/math/1/0/d/10d97baef8714cd0982a87681cfe4d1f.png)
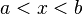
![]-\infty, b[ \ \ \mathrm{ \acute o } \ \ (- \infty, b) \!](http://upload.wikimedia.org/math/0/9/7/097e7c70e6cbf2559d82fcb85f853033.png)
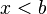
![]-\infty, b] \ \ \mathrm{ \acute o } \ \ (- \infty, b] \!](http://upload.wikimedia.org/math/e/8/2/e82cc38f6052cb558df6d0be418c5659.png)
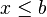
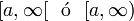
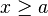
![]a, \infty [ \ \ \mathrm{ \acute o } \ \ (a, \infty ) \!](http://upload.wikimedia.org/math/7/6/7/767d79359e390fb402d696537c7d6b24.png)
![]\infty, + \infty [ \ \ \mathrm{ \acute o } \ \ (\infty, + \infty ) \!](http://upload.wikimedia.org/math/6/b/a/6ba8dc9071eaad7acf515f333bba45cf.png)
