si x e y pertenecen a I, x ≤ y, entonces para todo z tal que x ≤ z ≤ y, z pertenece a I. |
Se pueden clasificar los intervalos según sus características topológicas (intervalos abiertos, cerrados y semi abiertos) o según sus características métricas (su longitud: nula, finita no nula, o infinita).
Aquí están todos los casos posibles, con a ≤ b, y x perteneciente al intervalo, y l su longitud:
-------------------------------------------------------------------------------------------------------------
| Notación | Intervalo | Descripción | |
|---|---|---|---|
![[a, b] \,](http://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) | 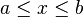 | Intervalo cerrado de longitud finita. | |
 | 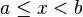 | Intervalo cerrado en a, abierto en b (semicerrado, semiabierto). | |
![]a, b] \ \ \mathrm{ \acute o } \ \ (a, b] \!](http://upload.wikimedia.org/math/0/1/8/0189f84b7a0ea78dbc527c545d8c9598.png) |  | intervalo abierto en a, cerrado en b. | |
![]a, b[ \ \ \mathrm{ \acute o } \ \ (a, b) \!](http://upload.wikimedia.org/math/1/0/d/10d97baef8714cd0982a87681cfe4d1f.png) | 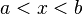 | intervalo abierto. | |
![]-\infty, b[ \ \ \mathrm{ \acute o } \ \ (- \infty, b) \!](http://upload.wikimedia.org/math/0/9/7/097e7c70e6cbf2559d82fcb85f853033.png) | 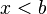 | Intervalo (semi) abierto. | |
![]-\infty, b] \ \ \mathrm{ \acute o } \ \ (- \infty, b] \!](http://upload.wikimedia.org/math/e/8/2/e82cc38f6052cb558df6d0be418c5659.png) | 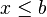 | Intervalo (semi) cerrado. | |
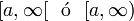 | 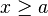 | Intervalo (semi) cerrado. | |
![]a, \infty [ \ \ \mathrm{ \acute o } \ \ (a, \infty ) \!](http://upload.wikimedia.org/math/7/6/7/767d79359e390fb402d696537c7d6b24.png) |  | Intervalo (semi) abierto. | |
![]\infty, + \infty [ \ \ \mathrm{ \acute o } \ \ (\infty, + \infty ) \!](http://upload.wikimedia.org/math/6/b/a/6ba8dc9071eaad7acf515f333bba45cf.png) | 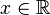 | Intervalo a la vez abierto y cerrado. | |
 |  | intervalo cerrado de longitud nula. Es un conjunto unitario. | |
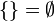 | x no existe | conjunto vacío. |
No hay comentarios:
Publicar un comentario